Published 2020-02-29

Understanding ISTA as a Fixed-Point Iteration

Background: Sparse Coding and Basis Pursuit Denoising

Sparse coding is an area of signal processing concerned with finding the representation of a signal with respect to a dictionary of vectors or atoms with the fewest number of coefficients. The assumption is that in some transform domains a signal ought to have only a few non-zero coefficients. Some simple examples of sparsity with respect to certain transforms are:

• complex sine-waves in the Fourier domain

• natural images in the DCT and Wavelet coefficient domains

Clearly sparsity is not a bad prior for many classes of signals. With redundant/over-complete dictionaries we can expect even greater sparsity in representation as the atom diversity can bring us closer to our signal in fewer combinations. This is similar to how the redundancy in human languages (synonyms etc.) allows ideas to be expressed very concisely.

Compression tasks and inverse problems (denoising, in-painting, deblurring, etc.) can benefit from sparse-coding in a redundant dictionary. Basis Pursuit DeNoising (BPDN) is one characterization of the sparse-coding objective in which we seek to minimize the $\ell_1$ taxi-cab norm of our transform coefficients as a convex-surrogate to the $\ell_0$ counting-norm (pseudo-norm). The BPDN objective can be written as

$$\text{minimize }\frac{1}{2} \lVert Ax-y \rVert_2^2 + \lambda \lVert x \rVert_1,$$

where $y$ is our signal, $A$ is our dictionary, $x$ is our sparse-representation or sparse-code, and $\lambda$ is a Lagrange multiplier term that balances the data-fidelity term and code sparsity.

The Iterative Soft-Thresholding Algorithm (ISTA)

Today, ISTA is by no means the best solution for solving the BPDN problem. However, it is very simple, easy to implement, and a good starting point for understanding this realm of optimization.

In its most common form, ISTA is written as,

Input: $A \in \mathbb{R}^{m\times n}, y \in \mathbb{R}^{m}$. Initialize: $x^0 \in \mathbb{R}^n$.

While not converged, repeat: $$x^{k+1} \coloneqq \mathcal{S}_{\lambda/L}\left( x^k - \tfrac{1}{L}A^T(Ax^k - y) \right)$$

return $x^{k+1}$

where $\mathcal{S}_{\alpha}$ is the soft-thresholding operator with cutoff parameter $\alpha$. We'll now walk through deriving ISTA by first deriving the Proximal Gradient Method – a fixed-point iteration – and then showing how ISTA is a special case.

Fixed-Point Iterations

Fixed point iterations (FPIs) can in general be characterized as repeating

$$x^{k+1} \coloneqq g(x^{k}),$$

for function $g: \mathbb{R}^n \rightarrow \mathbb{R}^n$. The contractive mapping theorem guarantees that this iterate will converge to the unique fixed point of $g$ given that $g$ is a contractive mapping (more on this next section).

For the purposes of optimization of a differentiable function $f$, we can exploit the FPI structure by rewriting $g$ as $g(x) = x - \Lambda \nabla f(x)$. As $\nabla f = 0$ at the extrema of $f$ they are all fixed points of $g$. If $\Lambda \nabla f$ is contractive, we can arrive at it's minima or maxima by a FPI on $g$.

Newton's Method does exactly this by replacing $\Lambda$ with the Jacobian of $f$ at $x^k$. The Gradient Descent algorithm does so with $\Lambda = \eta$, a learning rate set by the user before starting (which must be chosen carefully so as to not diverge).

Contractive Mappings

A mapping is called Lipschitz continuous if there exists a constant $L$ such that

$$\lVert f(x) - f(y) \rVert_2 \leq L \lVert x - y \rVert,$$

and is further called a contractive mapping if the Lipschitz constant $L < 1$. Intuitively we see that a contractive map is one where the distance between points becomes closer upon application, and that such a map could eventually bring us to a point that maps to itself (upon repeated application).

The Lipschitz constant $L$ will be brought up often in the discussion of ISTA. When known, it can be used to ensure that a function is contractive by scaling said function by $1/L$!

Proximal Operators and The Proximal Gradient Method

The area of proximal algorithms is built off of a nice mathematical object called the proximal operator, defined as

$$\mathbf{prox}_{\lambda f}(v) = \underset{x}{\mathrm{argmin }} \left(f(x) + \frac{1}{2\lambda}\lVert x-v \rVert_2^2 \right), \quad \lambda > 0$$

with parameter $\lambda$ for functional $f$.

A nice property of this operator is that $x^*$ minimizes the functional $f$ if and only if it is a fixed point of $\mathbf{prox}_{\lambda f}$, i.e., $x^* = \mathbf{prox}_{\lambda f}(x^*)$.

Derivation of the Proximal Operator for the $\ell_1$-Norm

As an example, let's derive the proximal operator for $f(x) = \lVert x \rVert_1$,

$$\begin{aligned} \mathbf{prox}_{\lambda f}(v) &= \underset{x}{\mathrm{argmin}} \left( \lVert x \rVert_1 + \frac{1}{2\lambda}\lVert x-v \rVert_2^2 \right) \cr &= \underset{x}{\mathrm{argmin}} \varphi(x,v) \qquad \end{aligned}$$

To find the minimum of $\varphi$ we differentiate element-wise with respect to $x$ and set the result equal to zero,

$$\begin{aligned} \varphi(x,v) &= \sum_{i=1}^n |x_i| + \frac{1}{2\lambda} \sum_{i=1}^n (x_i-v_i)^2 \cr \frac{\partial \varphi}{\partial x_i} &= \mathrm{sign}(x_i) + \frac{1}{\lambda} (x_i-v_i) = 0 \\ v_i &= \lambda \mathrm{sign}(x_i) + x_i \\ &= \begin{cases} x_i - \lambda & x_i < 0 \\ x_i + \lambda & x_i > 0 \end{cases} \end{aligned}$$

This corresponds to the following graph,

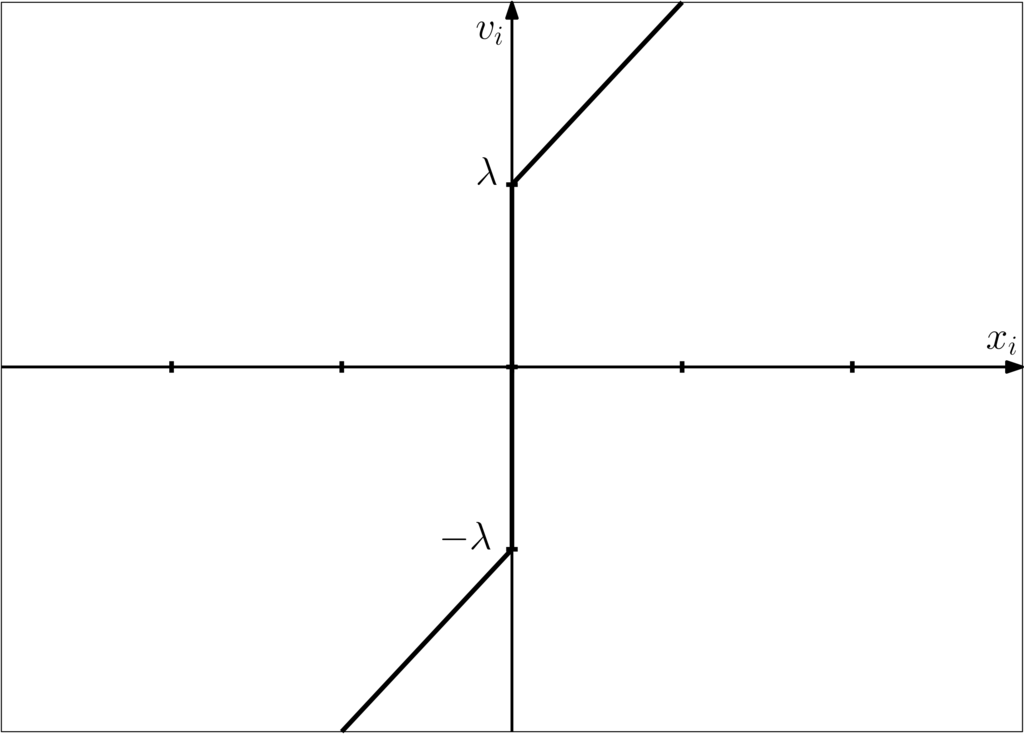
Either algebraically or graphically we may then obtain the following piecewise representation for $x_i$ in terms of $v_i$,

$$\begin{aligned} x_i = \begin{cases} v_i + \lambda,& v_i < -\lambda \\ 0,& |v_i| \leq \lambda \cr v_i - \lambda,& v_i > \lambda \\ \end{cases} \end{aligned}$$

This corresponds to the element-wise soft-thresholding operator, $\mathcal{S}_{\lambda}$, shown below.

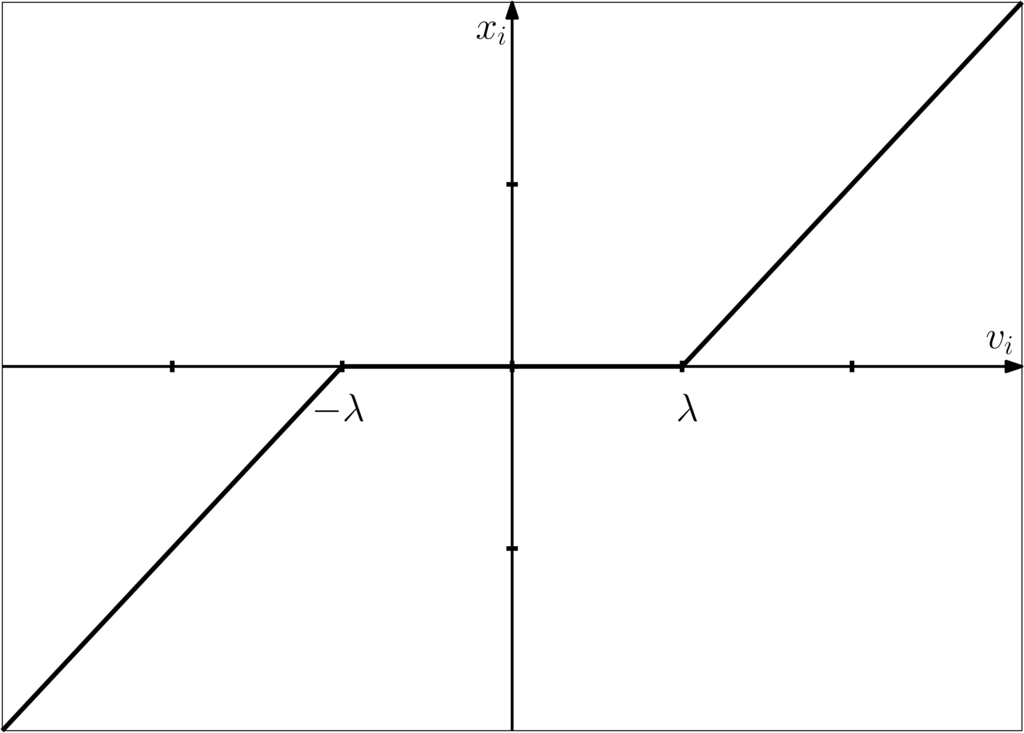
The soft-thresholding operator may be written more compactly as

$$\mathcal{S}_{\lambda}(u) = \mathrm{sign}(u)\max(|u|-\lambda,0),$$

or in Deep-Learning notation as

$$\mathcal{S}_{\lambda}(u) = \mathrm{sign}(u)\mathrm{relu}(|u|-\lambda).$$

Thus we have derived the proximal operator for the $\ell_1$ vector-norm to be the element-wise soft-thresholding operator (also known as the shrinkage-thresholding operator).

$$\mathrm{\textbf{prox}}_{\lambda f}(v) = \mathcal{S}_{\lambda}(v)$$

The Subdifferential

In order to continue our derivation of ISTA it is helpful for us to look at the proximal operator from a different perspective. First recall that the subdifferential $\partial f(x_0) \subset \mathbb{R}^n$ of convex function at point $x_0$ is the set defined as

$$\partial f(x_0) = \{y \,|\, f(x) - f(x_0) \geq y^T(x-x_0), \forall x \in \mathbf{dom} f\},$$

i.e., the set of slopes $y$ for which the hyperplanes at $x_0$ remain below the function. This allows us to generalize the idea of derivatives to convex functions that are non-smooth (not differentiable everywhere).

For instance, we know that a differentiable convex function has a global minimum at $x_0$ if and only if its gradient is zero, $\nabla f(x_0) = 0$. Similarly this is the case for a non-smooth convex function if and only if zero is in the subdifferential, $0 \in \partial f(x_0)$. Note that the subdifferential is equal to the gradient at a differentiable point.

Example: $f(x) = |x|$

• $\partial f(0) = \{y | -1 \leq y \leq 1 \}$

• $x_0 = 0$ is the global minimizer of $f$ as $0 \in \partial f(x_0)$

Resolvent of the Subdifferential

Theorem: With some restrictions on convex function $f$, the proximal operator is related to the subdifferential by

$$\mathbf{prox}_{\lambda f} = (I + \lambda \partial f)^{-1}.$$

The inverse set-relation $(I + \lambda \partial f)^{-1}$ is referred to as the resolvent of the subdifferential.

Proof Boyd (3.4): Consider $z \in (I + \lambda \partial f)^{-1}(x)$. Then,

$$\begin{aligned} x &\in (I + \lambda \partial f)(z) = z + \lambda \partial f(z) \cr 0 &\in \frac{1}{\lambda}(z-x) + \partial f(z) \cr \Leftrightarrow z &= {\underset{u}{\mathrm{argmin}\,}\,} \frac{1}{2\lambda} {\lVert u-x \rVert_2^2} + f(u) \cr z &= \mathbf{prox}_f(x) \qquad \Box \end{aligned}$$

Note that this shows that the set-relation $(I + \lambda \partial f)^{-1}(x)$ for $f$ convex is single-valued, as the proximal operator is a single-valued function.

The Proximal Gradient Method

Armed with our understanding of the proximal operator, the subdifferential, and the prox-op's characterization as the resolvent of the subdifferential, we can continue on our journey to derive ISTA by deriving The Proximal Gradient Method (Boyd Sec 4.2.1).

First, we will state the method. Consider the following optimization problem:

$$\text{minimize } f(x) + g(x)$$

with $f \text{ and } g$ both convex functionals and $f$ differentiable. The proximal gradient method

$$x^{k+1} \coloneqq \mathbf{prox}_{\eta g}(x^k - \eta \nabla f(x^k)),$$

is a fixed point iteration that converges to the unique minimizer of the objective function $f(x) + g(x)$ for a fixed step-size $\eta \in (0, 1/L]$, where $L$ is the Lipschitz constant of $\nabla f$. It can be shown that the algorithm converges as $\mathcal{O}(1/k)$ – very slow!

This can be seen from the necessary and sufficient condition that $x^{\star}$ is a minimizer of $f+g$ if and only if zero is in its subdifferential,

$$\begin{aligned} 0 &\in \eta \partial (f + g)(x^{\star}), \quad \eta > 0 \cr 0 &\in \eta \nabla f(x^{\star}) + \eta \partial g(x^{\star}) \cr 0 &\in \eta \nabla f(x^{\star}) + x^{\star} - x^{\star} + \eta \partial g(x^{\star}) \cr (I + \eta\partial g)(x^{\star}) &\ni (I - \eta\nabla f)(x^{\star}) \cr x^{\star} &= (I + \eta\partial g)^{-1}(I - \eta \nabla f)(x^{\star}) \cr x^{\star} &= \mathbf{prox}_{\eta g}(x^{\star} - \eta \nabla f(x^{\star})) \end{aligned}$$

We've used the fact that the proximal operator is the resolvent of the subdifferential to move from the containment relation to one of equality. The operator

$$(I + \eta\partial g)^{-1}(I - \eta \nabla f)$$

is referred to as the forward-backward operator. The proximal gradient method as shown applies the forward-backward operator in a fixed-point iteration to minimize $f+g$.

ISTA Assembled

We're now ready to assemble the Iterative Soft-Thresholding Algorithm. We'll restate the objective for convenience,

$$\text{minimize } \frac{1}{2} \lVert Ax-y \rVert_2^2 + \lambda \lVert x \rVert_1$$

where $A \in \mathbb{R}^{n \times m}, m >> n$, i.e. a fat/over-complete dictionary, $y \in \mathbb{R}^n$ is our signal, and $x \in \mathbb{R}^m$ is our sparse code to be determined.

If we label the quadratic term as $f$ and the relaxed sparsity term as $g$, we can use the proximal gradient method to get the update step

$$x^{k+1} \coloneqq \mathcal{S}_{\lambda \eta}( x^k - \eta A^T(Ax^k -y))$$

where $\mathcal{S}_{\lambda}$ is the proximal operator for the $\ell_1$ norm, soft-thresholding with parameter $\lambda$, as derived earlier.

More often, the ISTA update step is presented as

$$x^{k+1} \coloneqq \mathcal{S}_{\lambda/L}\left( x^k - \tfrac{1}{L}A^T(Ax^k -y)\right)$$

where $L = \sigma_{\mathrm{max}}(A)^2$, the square of the maximum singular value of $A$, i.e. the largest eigen-value of and Lipschitz constant of $A^TA$. This is simply ISTA with its fixed maximum step-size, ensuring that $A^TA \text{ and } \nabla f$ in turn are contractive.

In sum, ISTA is a fixed-point iteration on the forward-backward operator defined by the soft-thresholding (prox-op of the $\ell_1$ norm) and the gradient of the quadratic difference between the original signal and its sparse-code reconstruction. The threshold and step-size of the algorithm are determined by the sparsity-fidelity trade-off required by the problem and the maximum scaling possible in the dictionary.

Going Further

• Can we train an Artificial Neural Network to do ISTA faster? (Yes!) – LISTA

• Why are we still talking about ISTA when other algorithms do better?! – ADMM

• Why has the Relu appeared outside of a Deep-Learning context? – Elad