The Convolutional Dictionary Learning Network

Project Overview
Generalization in Denoising
Gabor is Enough!

Latest Updates:

May 2022:
- "Gabor is Enough" accepted into IVMSP 2022.
- CDLNet + GDLNet PyTorch code publicly available here
April 2022:
- CDLNet accepted into the IEEE Open Journal of Signal Processing!
- Preprint published: "Gabor is Enough: Interpretable Deep Denoising with a Gabor Synthesis Dictionary Prior".

Sparse representation is a proven and powerful prior for natural images and restoration tasks (such as denoising, deblurring, in-painting, etc.) involving them. More than simply finding these representations, learning an over-complete dictionary for sparse signal representation from degraded signals have been shown to be effective models. Furthermore, the convolutional dictionary learning (CDL) model seeks to represent the global signal via a translated local dictionary. This offers a more holistic approach for natural image representation compared to inherently suboptimal patch-processing methods. The dictionary learning problem is traditionally solved by iteratively compute spare-codes (representations) for a fixed dictionary, and subsequently updating the dictionary accordingly.

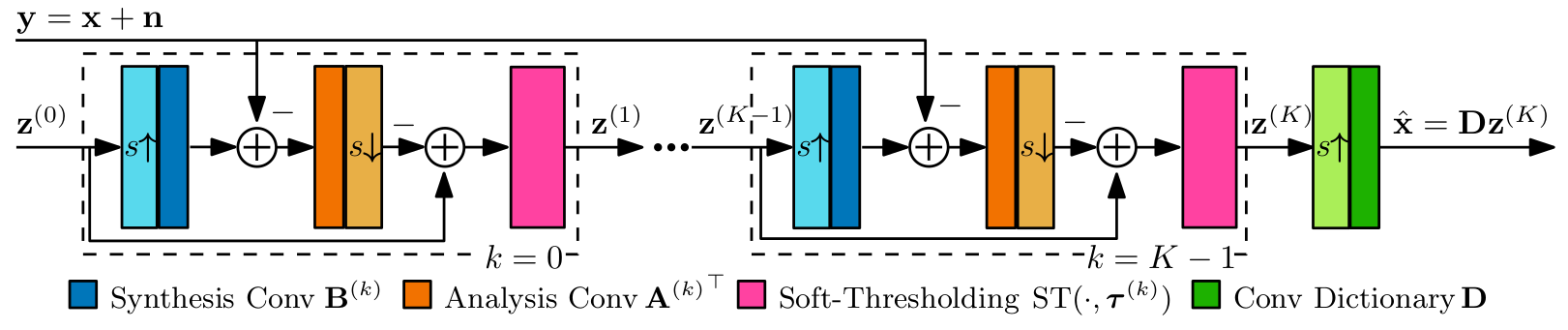
In this project, we explore an interpretable Deep Learning architecture for image restoration based on an unrolled CDL model. More specifically, we leverage the LISTA framework to obtain approximate convolutional sparse codes, followed by a synthesis from a convolutional dictionary. We call this architecture CDLNet. The network is trained in a task-driven fashion, amenable to any linear inverse-problem. We believe that interpretable network construction will yield greater insight and novel capabilities.

Participants

Yao Wang, Advising Professor, Lab Page
Nikola Janjušević, Ph.D. student
Amir Khalilian, Ph.D. student

Generalization in Denoising

The derivation of the CDLNet architecture allows us to understand the subband thresholds, $\tau^{(k)} \in \mathbb R_+^M$ , of the soft-thresholding operator as implicitly being a function of the input noise-level $\sigma$ . We thus propose an affine parameterization,

\tau^{(k)} = \tau_0^{(k)} + \tau_1^{(k)}\sigma

to explicitly model noise-level adaptivity within each layer of the network. This is in stark contrast to the implicitly defined noise-level adaptivity of common black-box neural networks, which either account for noise only via training on a noise range (ex. DnCNN), or additionally presented the estimated input noise-level as an input to the network (ex. FFDNet). As shown in the figures below, CDLNet's explicitly defined noise-level adaptivity allows for near-perfect generalization outside its training range, whereas the black box models either fail or introduce artifacts.

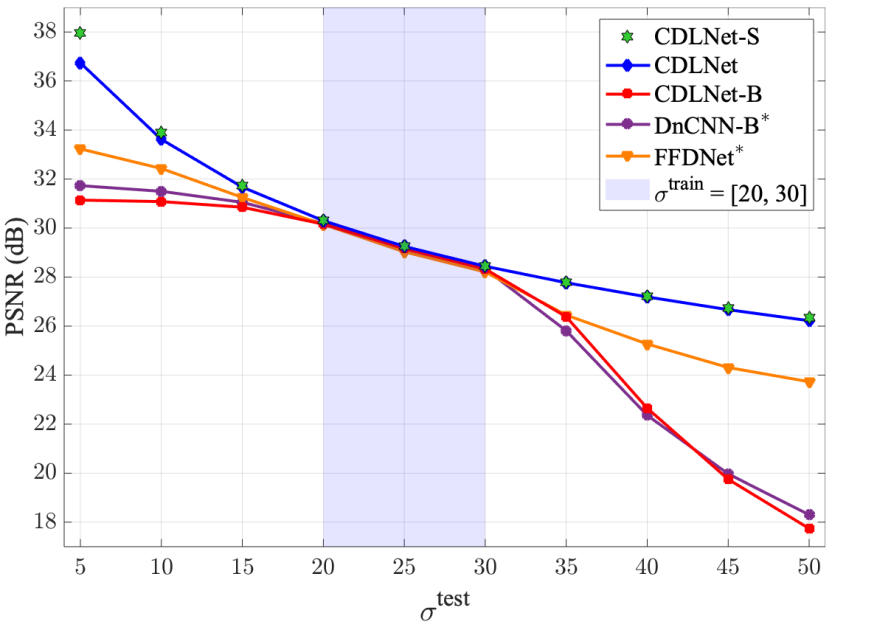
CDLNet is able to generalize outside its training noise-level range, whereas black-box neural networks fail.

This generalization characteristic is further demonstrated for the CDLNet architecture extended to color image denoising, joint-denoising-and-demosaicing, and unsupervised learning of denoising.

Joint Denoising and Demosaicing

CDLNet extended to the JDD task is able to achieve state-of-the-art results with a single model, out-performing black box neural networks.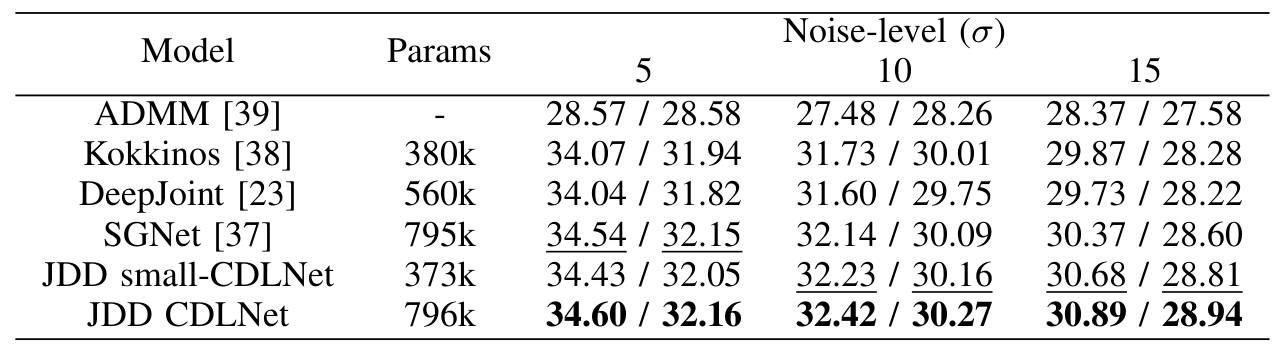

PSNR comparison against state-of-the-art JDD models on the Urban100/MIT moire datasets

The results of this section are detailed in, "CDLNet: Noise-Adaptive Convolutional Dictionary Learning Network for Blind Denoising and Demosaicing".

See our supplementary material with animations of filters, thresholds, and sparse codes across layers.

Gabor is Enough!

The GDLNet architecture with Mixture of Gabor filters.

Gabor filters (Gaussian $\times$ cosine) have a long history neural networks. Cat eye-cells have been shown to have Gabor-like frequency responses, and the learned filters at the early stages of the AlexNet classifier are noted to be Gabor-like as well. We noticed that the trained filters of CDLNet also appear Gabor-like and wondered, "Can Gabor-like be replaced with Gabor?". And so we parameterized each and every filter of CDLNet as a 2D real Gabor function,

g(\mathbf{x}; \phi) = \alpha e^{-\lVert \mathbf{a} \circ \mathbf{x} \rVert_2^2} \cos(\mathbf{\omega}_0^T \mathbf{x} + \psi),

with $\phi = (\alpha, \mathbf{a}, \mathbf{\omega}_0, \psi) \in \mathbb R^6$ as learnable parameters. We also considered mixture of Gabor (MoG) filters, i.e. each filter as sum of Gabor filters. We call this network GDLNet. Surprisingly, with just MoG=1, GDLNet can achieve competitive results with state-of-the-art CNN denoisers (see table below).

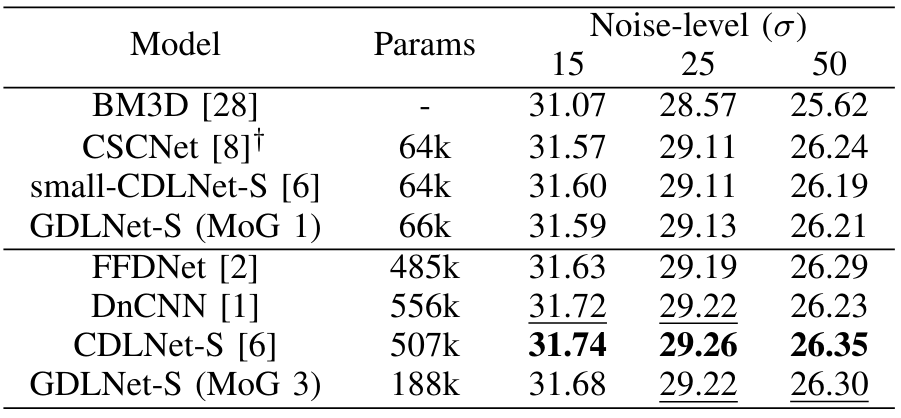
PSNR comparison against grayscale denoisers on BSD68 testset.

Our results suggest that the mechanisms behind low-level image processing neural networks need not be more complex than real Gabor filterbanks. Check out our preprint, "Gabor is Enough: Interpretable Deep Denoising with a Gabor Synthesis Dictionary Prior", for more results and information.