The following lecture notes are adapted from those of Karol Wadolowski (CU EE'19).

ECE 150 Digital Logic Design: Lesson 1

Table of Contents:

Numbering Systems
Arithmetic
1. Negative Numbers

Numbering Systems

Base 10 (decimal)

The base 10 system uses a total of 10 symbols (known as digits) in its (ordered) alphabet,

\mathcal{A} = \{0, 1, 2, 3, 4, 5, 6, 7 ,8, 9\}.

We express numbers via a combination of one or more of these symbols. Below we show how a decimal number written as a chain of symbols from the alphabet is implicitly represented using its base.

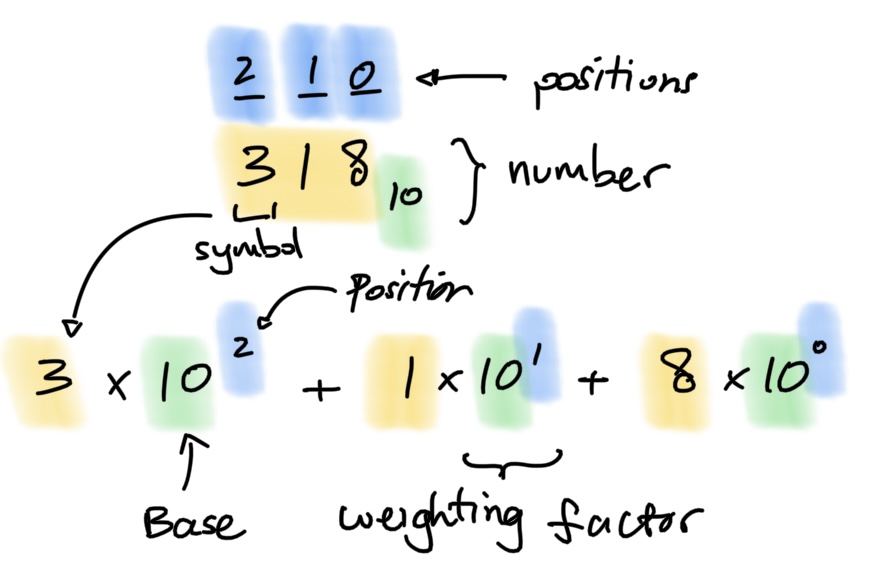
The position of each symbol encodes a weighting factor that is the base number raised to the power of the position. Fractional values are similarly represented by considering positions after the decimal point as negative indexed positions.

Example: A decimal number with fractional part

3.141_{10} = 3 \times 10^0 + 1 \times 10^{-1} + 4 \times 10^{-2} + 1 \times 10^{-3}

By convention, we call the left most digit the most significant digit as it is associated with the largest weighting factor. Similarly, the right most is called the least significant digit. Note that arithmetic between two numbers may change the number symbols required for representation, ex. $5_{10} + 6_{10} = 11_{10}$ .

What is the largest number we can represent with only 3 digits?

Base 2 (binary)

The use of 10 symbols in our decimal number system is somewhat arbitrary. What happens when we change our alphabet size to 2, i.e. $\mathcal{A} = \{0,1\}$ ? How would we represent our familiar decimal numbers?

Example: five in binary

\begin{array}{rcl} 101_2 &=& 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 \\ &=& 4 + 1 \\ &=& 5_{10} \end{array}

Again, the weighting factor is base of our number system (2) raised to the power of the symbol's position. We call the symbols in binary bits.

Reference: three bit numbers

\begin{array}{rcl} 0_{10} &=& 000_2 &~& 4_{10} &=& 100_2 \\ 1_{10} &=& 001_2 &~& 5_{10} &=& 101_2 \\ 2_{10} &=& 010_2 &~& 6_{10} &=& 110_2 \\ 3_{10} &=& 011_2 &~& 7_{10} &=& 111_2 \end{array}

We've already seen how to convert from binary to decimal using weighting factors. How about from decimal to binary? An intuitive way is to start with the largest power of 2 that fits into the number, and keep including powers of 2 until you've met the decimal number,

Example: intuitive decimal to binary

67_{10} = 64 + 2 + 1 = 2^6 + 2^1 + 2^0 = 0100~0011_2.

It's best to keep binary in groups of four bits for legibility, hence the leading zero.

A more algorithmic method for binary to decimal is to repeatedly divide the decimal number by two, recording the remainder, until zero is reached.

Example: sucessive division

\begin{array}{rcl} 67 \div 2 &=& 33, ~ &\text{rem.}& &1& ~\text{(LSB)} \\ 33 \div 2 &=& 16, ~ &\text{rem.}& &1& \\ 16 \div 2 &=& 8, ~ &\text{rem.}& &0& \\ 8 \div 2 &=& 4, ~ &\text{rem.}& &0& \\ 4 \div 2 &=& 2, ~ &\text{rem.}& &0& \\ 2 \div 2 &=& 1, ~ &\text{rem.}& &0& \\ 1 \div 2 &=& 0, ~ &\text{rem.}& &1& ~\text{(MSB)}\\ \end{array}

Hence, $67_{10} = 0100~0011_2$ .

Binary fractions: sucessive multiplication.
What' the largest number you can represent with $N$ bits?

Base 8 (octal) and Base 16 (hexadecimal)

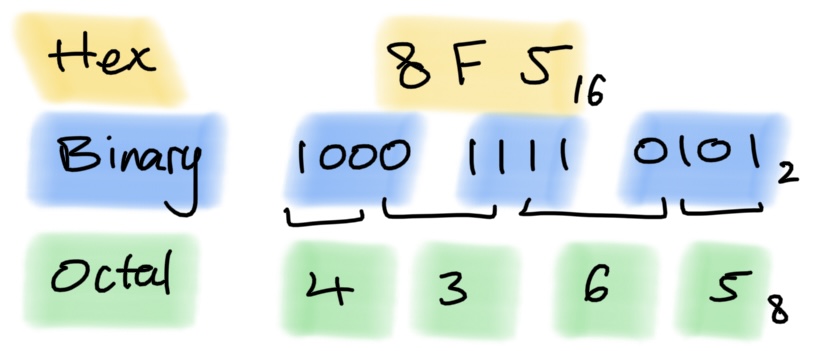
Reference: Common bases to 16

\begin{array}{rcl} \text{decimal} &~& \text{binary} &~& \text{octal} &~& \text{hex} \\\hline 0 &~& 0000 &~& 00 &~& 0 \\ 1 &~& 0001 &~& 01 &~& 1 \\ 2 &~& 0010 &~& 02 &~& 2 \\ 3 &~& 0011 &~& 03 &~& 3 \\\hline 4 &~& 0100 &~& 04 &~& 4 \\ 5 &~& 0101 &~& 05 &~& 5 \\ 6 &~& 0110 &~& 06 &~& 6 \\ 7 &~& 0111 &~& 07 &~& 7 \\\hline 8 &~& 1000 &~& 10 &~& 8 \\ 9 &~& 1001 &~& 11 &~& 9 \\ 10 &~& 1010 &~& 12 &~& A \\ 11 &~& 1011 &~& 13 &~& B \\\hline 12 &~& 1100 &~& 14 &~& C \\ 13 &~& 1101 &~& 15 &~& D \\ 14 &~& 1110 &~& 16 &~& E \\ 15 &~& 1111 &~& 17 &~& F \end{array}

Note that hexadecimal and octal have alphabet sizes of 16 and 8 respectivley. Our arabic digits don't go past nine, so we have to start using new symbols for hex.

An easy way to convert between hex and binary is by dealing with groups of 4 bits. Similarly octal numbers and 3 bits.

Binary Coded Decimal (BCD)

BCD represents each digit in a number separately in 4 bit binary.

Example: bcd

decimal           BCD
-------      --------------
  950   <--> 1001 0101 0000

Note: some bit patterns are invalid in BCD, ex. 1011 does not correspond to any decimal symbol.

It is useful for displaying information and interfacing with displays.

Arithmetic

The same tools of arithmetic you're familiar with in decimal carry over to other number systems. Most importantly, the tool of "carrying" extra symbols from one position to the next significant position when addition overflows.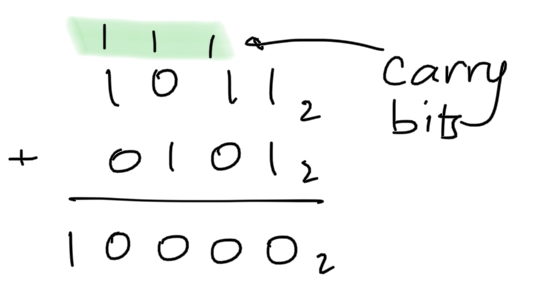

to extend your understanding, try:
- hex/octal addition/subtraction (without converting to binary)
- binary multiplication
- (hint) work through examples in decimal if you're stuck

Negative Numbers

How can we represent negative numbers? In everyday (decimal) life we use an extra symbol, the negative sign, ex. $-42$ . We call this representation sign-magnitude, and in binary it is represented by the MSB indicating the precense of a negative sign a.k.a the sign-bit.

Example: sign-magnitude binary

1110_2 = \underbrace{1}_{\text{sign}}\overbrace{110_2}^{\text{magnitude}} = -6_{10}

Given $N$ bits, what's the range of numbers spanned by a sign-magnitude representation?

Another (more common) way of representing sign in binary is via Two's Complement. In this representation, the weighting factor of the MSB is given a negative sign. Negation is conviently achieved by flipping bits and adding one.

Example: two's complement

1110_2 = -2^3 + 2^2 + 2^1 = -2_{10}

\overset{\text{flip}}{\rightarrow} ~ 0001_2 ~ \overset{\text{+1}}{\rightarrow} ~ 0010_2 = 2_{10}

This has the following benefits over sign-magnitude:

no negative zero, larger range
subtraction is equivalent to negation + addition (only one circuit required: addition)

Example: two's complement subtraction

We verify that addition arithmetic works two's complement numbers. Note that the final carry bit is ignored by design.

decimal         sign-mag.      2's comp.     decimal
-------        -----------    -----------    --------
           carry:              111 1   1
  45 =>          0010 1101 =>   0010 1101 
- 23           - 0001 0111    + 1110 1001
====           ===========    ===========
  22                           10001 0110
        ignore overflow:        0001 0110 => 22

A downside of two's complement is that underflow/overflow must be manually checked before computation begins, as opposed to being indicated via a carry bit. This is due to the "wrap-around" nature of the representation which is required for its nice arithmetic properties. For example, in two's complement,

7_{10} + 1_{10} = 0111_2 + 0001_2 = 1000_2 = -8_{10}.

extra terminology

bit: binary symbol (0 or 1)
byte: 8 bits
nibble: half a byte, 4 bits
kilo-byte (KB): 1,000 bytes = 8,000 bits
kilo-bit (Kb): 1,000 bits
- How fast will a 100 MB file download over your 100 Mbps internet connection?